
- History & Society
- Science & Tech
- Biographies
- Animals & Nature
- Geography & Travel
- Arts & Culture
- Games & Quizzes
- On This Day
- One Good Fact
- New Articles
- Lifestyles & Social Issues
- Philosophy & Religion
- Politics, Law & Government
- World History
- Health & Medicine
- Browse Biographies
- Birds, Reptiles & Other Vertebrates
- Bugs, Mollusks & Other Invertebrates
- Environment
- Fossils & Geologic Time
- Entertainment & Pop Culture
- Sports & Recreation
- Visual Arts
- Demystified
- Image Galleries
- Infographics
- Top Questions
- Britannica Kids
- Saving Earth
- Space Next 50
- Student Center


Where was Srinivasa Ramanujan educated?
- What are the oldest known civilizations of India?
- What are the major holidays and festivals of India?

Srinivasa Ramanujan
Our editors will review what you’ve submitted and determine whether to revise the article.
- Institute of Mathematics & its Applications - Biography of Srinivasa Ramanujan (1887–1920): The Centenary of a Remarkable Mathematician
- IndiaNetzone - Indian Personalities - Biography of Srinavasa Iyengar Ramanujan
- San José State University - Srinivasa Ramanujan, a mathematician brilliant beyond comparison
- U.S.Naval Institute - Srinivasa Ramanujan
- Linda Hall Library - Srinivasa Ramanujan
- Academia - Great Mathematician Ramanujan
- Srinivasa Ramanujan - Student Encyclopedia (Ages 11 and up)

At age 15 Srinivasa Ramanujan obtained a mathematics book containing thousands of theorems , which he verified and from which he developed his own ideas. In 1903 he briefly attended the University of Madras . In 1914 he went to England to study at Trinity College, Cambridge , with British mathematician G.H. Hardy .
What were Srinivasa Ramanujan’s contributions?
Indian mathematician Srinivasa Ramanujan made contributions to the theory of numbers , including pioneering discoveries of the properties of the partition function. His papers were published in English and European journals, and in 1918 he was elected to the Royal Society of London.
What is Srinivasa Ramanujan remembered for?
Srinivasa Ramanujan is remembered for his unique mathematical brilliance, which he had largely developed by himself. In 1920 he died at age 32, generally unknown to the world at large but recognized by mathematicians as a phenomenal genius, without peer since Leonhard Euler (1707–83) and Carl Jacobi (1804–51).
Srinivasa Ramanujan (born December 22, 1887, Erode , India—died April 26, 1920, Kumbakonam) was an Indian mathematician whose contributions to the theory of numbers include pioneering discoveries of the properties of the partition function.
When he was 15 years old, he obtained a copy of George Shoobridge Carr’s Synopsis of Elementary Results in Pure and Applied Mathematics, 2 vol. (1880–86). This collection of thousands of theorems , many presented with only the briefest of proofs and with no material newer than 1860, aroused his genius. Having verified the results in Carr’s book, Ramanujan went beyond it, developing his own theorems and ideas. In 1903 he secured a scholarship to the University of Madras but lost it the following year because he neglected all other studies in pursuit of mathematics .

Ramanujan continued his work, without employment and living in the poorest circumstances. After marrying in 1909 he began a search for permanent employment that culminated in an interview with a government official, Ramachandra Rao. Impressed by Ramanujan’s mathematical prowess, Rao supported his research for a time, but Ramanujan, unwilling to exist on charity, obtained a clerical post with the Madras Port Trust.
In 1911 Ramanujan published the first of his papers in the Journal of the Indian Mathematical Society . His genius slowly gained recognition, and in 1913 he began a correspondence with the British mathematician Godfrey H. Hardy that led to a special scholarship from the University of Madras and a grant from Trinity College , Cambridge . Overcoming his religious objections, Ramanujan traveled to England in 1914, where Hardy tutored him and collaborated with him in some research.
Ramanujan’s knowledge of mathematics (most of which he had worked out for himself) was startling. Although he was almost completely unaware of modern developments in mathematics, his mastery of continued fractions was unequaled by any living mathematician. He worked out the Riemann series, the elliptic integrals , hypergeometric series, the functional equations of the zeta function , and his own theory of divergent series, in which he found a value for the sum of such series using a technique he invented that came to be called Ramanujan summation. On the other hand, he knew nothing of doubly periodic functions, the classical theory of quadratic forms, or Cauchy’s theorem, and he had only the most nebulous idea of what constitutes a mathematical proof. Though brilliant, many of his theorems on the theory of prime numbers were wrong.
In England Ramanujan made further advances, especially in the partition of numbers (the number of ways that a positive integer can be expressed as the sum of positive integers; e.g., 4 can be expressed as 4, 3 + 1, 2 + 2, 2 + 1 + 1, and 1 + 1 + 1 + 1). His papers were published in English and European journals, and in 1918 he was elected to the Royal Society of London . In 1917 Ramanujan had contracted tuberculosis , but his condition improved sufficiently for him to return to India in 1919. He died the following year, generally unknown to the world at large but recognized by mathematicians as a phenomenal genius, without peer since Leonhard Euler (1707–83) and Carl Jacobi (1804–51). Ramanujan left behind three notebooks and a sheaf of pages (also called the “lost notebook”) containing many unpublished results that mathematicians continued to verify long after his death.
- IAS Preparation
- UPSC Preparation Strategy
- Srinivasa Ramanujan
Srinivasa Ramanujan (1887-1920)
One of the greatest mathematicians of all time, Srinivasa Ramanujan was born in 1887 in the Southern part of India. He is still remembered for his contributions to the field of mathematics. Theorems formulated by him are to date studied by students across the world and within very few years of his lifespan, he made some exceptional discoveries in mathematics.
His biography and achievements prove a lot about him and his struggles to contribute to the field of this subject. All this is also an essential part of the syllabus for aspirants preparing for the upcoming IAS Exam .
The facts, achievements and contributions presented by Srinivasa Ramanujan have not just been acknowledged within India, but also globally by leading mathematicians. Aspirants can also learn about other Indian mathematicians and their contributions , by visiting the linked article.
Srinivasa Ramanujan Biography [UPSC Notes]:- Download PDF Here
| Kickstart your preparation now! Complement it with the links given below: |
Indian Mathematician S. Ramanujan – Biography
Born in 1887, Ramanujan’s life, as said by Sri Aurobindo, was a “rags to mathematical riches” life story. His geniuses of the 20th century are still giving shape to 21st-century mathematics.
Discussed below is the history, achievements, contributions, etc. of Ramanujan’s life journey.
Birth –
- Srinivasa Ramanujan was born on 22nd December 1887 in the south Indian town of Tamil Nad, named Erode.
- His father, Kuppuswamy Srinivasa Iyengar worked as a clerk in a saree shop and his mother, Komalatamma was a housewife.
- Since a very early age, he had a keen interest in mathematics and had already become a child prodigy
Srinivasa Ramanujan Education –
- He attained his early education and schooling from Madras , where he was enrolled in a local school
- His love for mathematics had grown at a very young age and was mostly self-taught
- He was a promising student and had won many academic prizes in high school
- But his love for mathematics proved to be a disadvantage when he reached college. As he continued to excel in only one subject and kept failing in all others . This resulted in him dropping out of college
- However, he continued to work on his collection of mathematical theorems, ideologies and concepts until he got his final breakthrough
Final Break Through –
- S. Ramanujam did not keep all his discoveries to himself but continued to send his works to International mathematicians
- In 1912, he was appointed at the position of clerk in the Madras Post Trust Office, where the manager, S.N. Aiyar encouraged him to reach out to G.H. Hardy, a famous mathematician at the Cambridge University
- In 1913, he had sent the famous letter to Hardy, in which he had attached 120 theorems as a sample of his work
- Hardy along with another mathematician at Cambridge, J.E.Littlewood analysed his work and concluded it to be a work of true genius
- It was after this that his journey and recognition as one of the greatest mathematicians had started
Death –
- In 1919, Ramanujan’s health had started to deteriorate, after which he decided to move back to India
- After his return in 1920, his health further worsened and he died at the age of just 32 years
The life of such great Indians and their contribution in various fields is an important part of the UPSC Syllabus . Candidates preparing for the upcoming civil services exam must analyse this information carefully.
Other Related Links:
Srinivasa Ramanujan Contributions
- Between 1914 and 1914, while Ramanujan was in England, he along with Hardy published over a dozen research papers
- During the time period of three years, he had published around 30 research papers
- Hardy and Ramanujan had developed a new method, now called the circle method , to derive an asymptomatic formula for this function
- His first paper published, a 17-page work on Bernoulli numbers that appeared in 1911 in the Journal of the Indian Mathematical Society
- One remarkable result of the Hardy-Ramanujan collaboration was a formula for the number p(n) of partitions of a number ‘n’
Achievements of Srinivasa Ramanujan
- At the age of 12, he had completely read Loney’s book on Plane Trignimetry and A Synopsis of Elementary Results in Pure and Applied Mathematics , which were way beyond the standard of a high school student
- In 1916 , he was granted a Bachelor of Science degree “by research” at the Cambridge University
- In 1918 , he became the first Indian to be honoured as a Fellow of the Royal Society
- In 1997, The Ramanujan Journal was launched to publish work “in areas of mathematics influenced by Ramanujan”
- The year 2012 was declared as the National Mathematical Year as it marked the 125th birth year of one of the greatest Indian mathematicians
- Since 2021, his birth anniversary, December 22, is observed as the National Mathematicians Day every year in India
The intention behind encouraging the significance of mathematics was mainly to boost youngsters who are the future of the country and influence them to have a keen interest in analysing the scope of this subject.
Also, aspirants appearing in the civil services exam can choose mathematics as an optional and the success stories of IAS Toppers from the past have shown the scope of this subject.
To get details of UPSC 2024 , candidates can visit the linked article.
For any further information about the upcoming civil services examination , study material, preparation tips and strategy, candidates can visit the linked article.

| IAS General Studies Notes Links | |
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Request OTP on Voice Call
Post My Comment
Good biography
IAS 2024 - Your dream can come true!
Download the ultimate guide to upsc cse preparation, register with byju's & download free pdfs, register with byju's & watch live videos.
Srinivasa Ramanujan

(1887-1920)
Who Was Srinivasa Ramanujan?
After demonstrating an intuitive grasp of mathematics at a young age, Srinivasa Ramanujan began to develop his own theories and in 1911, he published his first paper in India. Two years later Ramanujan began a correspondence with British mathematician G. H. Hardy that resulted in a five-year-long mentorship for Ramanujan at Cambridge, where he published numerous papers on his work and received a B.S. for research. His early work focused on infinite series and integrals, which extended into the remainder of his career. After contracting tuberculosis, Ramanujan returned to India, where he died in 1920 at 32 years of age.
Srinivasa Ramanujan was born on December 22, 1887, in Erode, India, a small village in the southern part of the country. Shortly after this birth, his family moved to Kumbakonam, where his father worked as a clerk in a cloth shop. Ramanujan attended the local grammar school and high school and early on demonstrated an affinity for mathematics.
When he was 15, he obtained an out-of-date book called A Synopsis of Elementary Results in Pure and Applied Mathematics , Ramanujan set about feverishly and obsessively studying its thousands of theorems before moving on to formulate many of his own. At the end of high school, the strength of his schoolwork was such that he obtained a scholarship to the Government College in Kumbakonam.
A Blessing and a Curse
However, Ramanujan’s greatest asset proved also to be his Achilles heel. He lost his scholarship to both the Government College and later at the University of Madras because his devotion to math caused him to let his other courses fall by the wayside. With little in the way of prospects, in 1909 he sought government unemployment benefits.
Yet despite these setbacks, Ramanujan continued to make strides in his mathematical work, and in 1911, published a 17-page paper on Bernoulli numbers in the Journal of the Indian Mathematical Society . Seeking the help of members of the society, in 1912 Ramanujan was able to secure a low-level post as a shipping clerk with the Madras Port Trust, where he was able to make a living while building a reputation for himself as a gifted mathematician.
Around this time, Ramanujan had become aware of the work of British mathematician G. H. Hardy — who himself had been something of a young genius — with whom he began a correspondence in 1913 and shared some of his work. After initially thinking his letters a hoax, Hardy became convinced of Ramanujan’s brilliance and was able to secure him both a research scholarship at the University of Madras as well as a grant from Cambridge.
The following year, Hardy convinced Ramanujan to come study with him at Cambridge. During their subsequent five-year mentorship, Hardy provided the formal framework in which Ramanujan’s innate grasp of numbers could thrive, with Ramanujan publishing upwards of 20 papers on his own and more in collaboration with Hardy. Ramanujan was awarded a bachelor of science degree for research from Cambridge in 1916 and became a member of the Royal Society of London in 1918.
Doing the Math
"[Ramanujan] made many momentous contributions to mathematics especially number theory," states George E. Andrews, an Evan Pugh Professor of Mathematics at Pennsylvania State University. "Much of his work was done jointly with his benefactor and mentor, G. H. Hardy. Together they began the powerful "circle method" to provide an exact formula for p(n), the number of integer partitions of n. (e.g. p(5)=7 where the seven partitions are 5, 4+1, 3+2, 3+1+1, 2+2+1, 2+1+1+1, 1+1+1+1+1). The circle method has played a major role in subsequent developments in analytic number theory. Ramanujan also discovered and proved that 5 always divides p(5n+4), 7 always divides p(7n+5) and 11 always divides p(11n+6). This discovery led to extensive advances in the theory of modular forms."
But years of hard work, a growing sense of isolation and exposure to the cold, wet English climate soon took their toll on Ramanujan and in 1917 he contracted tuberculosis. After a brief period of recovery, his health worsened and in 1919 he returned to India.
The Man Who Knew Infinity
Ramanujan died of his illness on April 26, 1920, at the age of 32. Even on his deathbed, he had been consumed by math, writing down a group of theorems that he said had come to him in a dream. These and many of his earlier theorems are so complex that the full scope of Ramanujan’s legacy has yet to be completely revealed and his work remains the focus of much mathematical research. His collected papers were published by Cambridge University Press in 1927.
Of Ramanujan's published papers — 37 in total — Berndt reveals that "a huge portion of his work was left behind in three notebooks and a 'lost' notebook. These notebooks contain approximately 4,000 claims, all without proofs. Most of these claims have now been proved, and like his published work, continue to inspire modern-day mathematics."
A biography of Ramanujan titled The Man Who Knew Infinity was published in 1991, and a movie of the same name starring Dev Patel as Ramanujan and Jeremy Irons as Hardy, premiered in September 2015 at the Toronto Film Festival.
QUICK FACTS
- Name: Srinivasa Ramanujan
- Birth Year: 1887
- Birth date: December 22, 1887
- Birth City: Erode
- Birth Country: India
- Gender: Male
- Best Known For: Srinivasa Ramanujan was a mathematical genius who made numerous contributions in the field, namely in number theory. The importance of his research continues to be studied and inspires mathematicians today.
- Education and Academia
- Astrological Sign: Sagittarius
- University of Madras
- Cambridge University
- Nacionalities
- Death Year: 1920
- Death date: April 26, 1920
- Death City: Kumbakonam
- Death Country: India
We strive for accuracy and fairness.If you see something that doesn't look right, contact us !
CITATION INFORMATION
- Article Title: Srinivasa Ramanujan Biography
- Author: Biography.com Editors
- Website Name: The Biography.com website
- Url: https://www.biography.com/scientists/srinivasa-ramanujan
- Access Date:
- Publisher: A&E; Television Networks
- Last Updated: September 10, 2019
- Original Published Date: September 10, 2015
Watch Next .css-16toot1:after{background-color:#262626;color:#fff;margin-left:1.8rem;margin-top:1.25rem;width:1.5rem;height:0.063rem;content:'';display:-webkit-box;display:-webkit-flex;display:-ms-flexbox;display:flex;}

Famous Mathematicians

Archimedes: The Mathematician Who Discovered Pi

Benjamin Banneker

22 Famous Scientists You Should Know

Charles Babbage

Blaise Pascal

Leonhard Euler

Ada Lovelace

Valerie Thomas

Mary Jackson
MacTutor
Srinivasa aiyangar ramanujan.
A short uncouth figure, stout, unshaven, not over clean, with one conspicuous feature-shining eyes- walked in with a frayed notebook under his arm. He was miserably poor. ... He opened his book and began to explain some of his discoveries. I saw quite at once that there was something out of the way; but my knowledge did not permit me to judge whether he talked sense or nonsense. ... I asked him what he wanted. He said he wanted a pittance to live on so that he might pursue his researches.
I have passed the Matriculation Examination and studied up to the First Arts but was prevented from pursuing my studies further owing to several untoward circumstances. I have, however, been devoting all my time to Mathematics and developing the subject.
I can strongly recommend the applicant. He is a young man of quite exceptional capacity in mathematics and especially in work relating to numbers. He has a natural aptitude for computation and is very quick at figure work.
I have had no university education but I have undergone the ordinary school course. After leaving school I have been employing the spare time at my disposal to work at mathematics. I have not trodden through the conventional regular course which is followed in a university course, but I am striking out a new path for myself. I have made a special investigation of divergent series in general and the results I get are termed by the local mathematicians as 'startling'.
I was exceedingly interested by your letter and by the theorems which you state. You will however understand that, before I can judge properly of the value of what you have done, it is essential that I should see proofs of some of your assertions. Your results seem to me to fall into roughly three classes: (1) there are a number of results that are already known, or easily deducible from known theorems; (2) there are results which, so far as I know, are new and interesting, but interesting rather from their curiosity and apparent difficulty than their importance; (3) there are results which appear to be new and important...
I have found a friend in you who views my labours sympathetically. ... I am already a half starving man. To preserve my brains I want food and this is my first consideration. Any sympathetic letter from you will be helpful to me here to get a scholarship either from the university of from the government.
What was to be done in the way of teaching him modern mathematics? The limitations of his knowledge were as startling as its profundity.
... that it was extremely difficult because every time some matter, which it was thought that Ramanujan needed to know, was mentioned, Ramanujan's response was an avalanche of original ideas which made it almost impossible for Littlewood to persist in his original intention.
Batty Shaw found out, what other doctors did not know, that he had undergone an operation about four years ago. His worst theory was that this had really been for the removal of a malignant growth, wrongly diagnosed. In view of the fact that Ramanujan is no worse than six months ago, he has now abandoned this theory - the other doctors never gave it any support. Tubercle has been the provisionally accepted theory, apart from this, since the original idea of gastric ulcer was given up. ... Like all Indians he is fatalistic, and it is terribly hard to get him to take care of himself.
I think we may now hope that he has turned to corner, and is on the road to a real recovery. His temperature has ceased to be irregular, and he has gained nearly a stone in weight. ... There has never been any sign of any diminuation in his extraordinary mathematical talents. He has produced less, naturally, during his illness but the quality has been the same. .... He will return to India with a scientific standing and reputation such as no Indian has enjoyed before, and I am confident that India will regard him as the treasure he is. His natural simplicity and modesty has never been affected in the least by success - indeed all that is wanted is to get him to realise that he really is a success.
References ( show )
- O Ore, Biography in Dictionary of Scientific Biography ( New York 1970 - 1990) . See THIS LINK .
- Biography in Encyclopaedia Britannica. http://www.britannica.com/biography/Srinivasa-Ramanujan
- B C Berndt and R A Rankin, Ramanujan : Letters and commentary ( Providence, Rhode Island, 1995) .
- G H Hardy, Ramanujan ( Cambridge, 1940) .
- R Kanigel, The man who knew infinity : A life of the genius Ramanujan ( New York, 1991) .
- J N Kapur ( ed. ) , Some eminent Indian mathematicians of the twentieth century ( Kapur, 1989) .
- S Ram, Srinivasa Ramanujan ( New Delhi, 1979) .
- S Ramanujan, Collected Papers ( Cambridge, 1927) .
- S R Ranganathan, Ramanujan : the man and the mathematician ( London, 1967) .
- P K Srinivasan, Ramanujan : Am inspiration 2 Vols. ( Madras, 1968) .
- P V Seshu Aiyar, The late Mr S Ramanujan, B.A., F.R.S., J. Indian Math. Soc. 12 (1920) , 81 - 86 .
- G E Andrews, An introduction to Ramanujan's 'lost' notebook, Amer. Math. Monthly 86 (1979) , 89 - 108 .
- B Berndt, Srinivasa Ramanujan, The American Scholar 58 (1989) , 234 - 244 .
- B Berndt and S Bhargava, Ramanujan - For lowbrows, Amer. Math. Monthly 100 (1993) , 644 - 656 .
- B Bollobas, Ramanujan - a glimpse of his life and his mathematics, The Cambridge Review (1988) , 76 - 80 .
- B Bollobas, Ramanujan - a glimpse of his life and his mathematics, Eureka 48 (1988) , 81 - 98 .
- J M Borwein and P B Borwein, Ramanujan and pi, Scientific American 258 (2) (1988) , 66 - 73 .
- S Chandrasekhar, On Ramanujan, in Ramanujan Revisited ( Boston, 1988) , 1 - 6 .
- L Debnath, Srinivasa Ramanujan (1887 - 1920) : a centennial tribute, International journal of mathematical education in science and technology 18 (1987) , 821 - 861 .
- G H Hardy, The Indian mathematician Ramanujan, Amer. Math. Monthly 44 (3) (1937) , 137 - 155 .
- G H Hardy, Srinivasa Ramanujan, Proc. London Math, Soc. 19 (1921) , xl-lviii.
- E H Neville, Srinivasa Ramanujan, Nature 149 (1942) , 292 - 294 .
- C T Rajagopal, Stray thoughts on Srinivasa Ramanujan, Math. Teacher ( India ) 11 A (1975) , 119 - 122 , and 12 (1976) , 138 - 139 .
- K Ramachandra, Srinivasa Ramanujan ( the inventor of the circle method ) , J. Math. Phys. Sci. 21 (1987) , 545 - 564 .
- K Ramachandra, Srinivasa Ramanujan ( the inventor of the circle method ) , Hardy-Ramanujan J. 10 (1987) , 9 - 24 .
- R A Rankin, Ramanujan's manuscripts and notebooks, Bull. London Math. Soc. 14 (1982) , 81 - 97 .
- R A Rankin, Ramanujan's manuscripts and notebooks II, Bull. London Math. Soc. 21 (1989) , 351 - 365 .
- R A Rankin, Srinivasa Ramanujan (1887 - 1920) , International journal of mathematical education in science and technology 18 (1987) , 861 -.
- R A Rankin, Ramanujan as a patient, Proc. Indian Ac. Sci. 93 (1984) , 79 - 100 .
- R Ramachandra Rao, In memoriam S Ramanujan, B.A., F.R.S., J. Indian Math. Soc. 12 (1920) , 87 - 90 .
- E Shils, Reflections on tradition, centre and periphery and the universal validity of science : the significance of the life of S Ramanujan, Minerva 29 (1991) , 393 - 419 .
- D A B Young, Ramanujan's illness, Notes and Records of the Royal Society of London 48 (1994) , 107 - 119 .
Additional Resources ( show )
Other pages about Srinivasa Ramanujan:
- Multiple entries in The Mathematical Gazetteer of the British Isles ,
- Miller's postage stamps
- Heinz Klaus Strick biography
Other websites about Srinivasa Ramanujan:
- Dictionary of Scientific Biography
- Dictionary of National Biography
- Encyclopaedia Britannica
- Ramanujan's last letter
- Srinivasa Rao
- Plus Magazine
- A Sen ( An article about the influence of Carr's book on Ramanujan )
- Kevin Brown ( Something else about 1729)
- The mathematician and his legacy ( YouTube video )
- Sci Hi blog
- Google doodle
- Mathematical Genealogy Project
- MathSciNet Author profile
- zbMATH entry
Honours ( show )
Honours awarded to Srinivasa Ramanujan
- Fellow of the Royal Society 1918
- Popular biographies list Number 1
- Google doodle 2012
Cross-references ( show )
- History Topics: Squaring the circle
- Famous Curves: Ellipse
- Societies: Indian Academy of Sciences
- Societies: Indian Mathematical Society
- Societies: Ramanujan Mathematical Society
- Other: 16th March
- Other: 1st April
- Other: 2009 Most popular biographies
- Other: 22nd December
- Other: 27th February
- Other: 8th February
- Other: Cambridge Colleges
- Other: Cambridge Individuals
- Other: Earliest Known Uses of Some of the Words of Mathematics (D)
- Other: Earliest Known Uses of Some of the Words of Mathematics (H)
- Other: Jeff Miller's postage stamps
- Other: London Learned Societies
- Other: London individuals N-R
- Other: Most popular biographies – 2024
- Other: Oxford individuals
- Other: Popular biographies 2018
Biography of Srinivasa Ramanujan, Mathematical Genius
Public Domain
- Famous Inventors
- Famous Inventions
- Patents & Trademarks
- Invention Timelines
- Computers & The Internet
- American History
- African American History
- African History
- Ancient History and Culture
- Asian History
- European History
- Latin American History
- Medieval & Renaissance History
- Military History
- The 20th Century
- Women's History
- Ph.D., Materials Science and Engineering, Northwestern University
- B.A., Chemistry, Johns Hopkins University
- B.A., Cognitive Science, Johns Hopkins University
Srinivasa Ramanujan (born December 22, 1887 in Erode, India) was an Indian mathematician who made substantial contributions to mathematics—including results in number theory, analysis, and infinite series—despite having little formal training in math.
Fast Facts: Srinivasa Ramanujan
- Full Name: Srinivasa Aiyangar Ramanujan
- Known For: Prolific mathematician
- Parents’ Names: K. Srinivasa Aiyangar, Komalatammal
- Born: December 22, 1887 in Erode, India
- Died: April 26, 1920 at age 32 in Kumbakonam, India
- Spouse: Janakiammal
- Interesting Fact: Ramanujan's life is depicted in a book published in 1991 and a 2015 biographical film, both titled "The Man Who Knew Infinity."
Early Life and Education
Ramanujan was born on December 22, 1887, in Erode, a city in southern India. His father, K. Srinivasa Aiyangar, was an accountant, and his mother Komalatammal was the daughter of a city official. Though Ramanujan’s family was of the Brahmin caste , the highest social class in India, they lived in poverty.
Ramanujan began attending school at the age of 5. In 1898, he transferred to Town High School in Kumbakonam. Even at a young age, Ramanujan demonstrated extraordinary proficiency in math, impressing his teachers and upperclassmen.
However, it was G.S. Carr’s book, "A Synopsis of Elementary Results in Pure Mathematics," which reportedly spurred Ramanujan to become obsessed with the subject. Having no access to other books, Ramanujan taught himself mathematics using Carr’s book, whose topics included integral calculus and power series calculations. This concise book would have an unfortunate impact on the way Ramanujan wrote down his mathematical results later, as his writings included too few details for many people to understand how he arrived at his results.
Ramanujan was so interested in studying mathematics that his formal education effectively came to a standstill. At the age of 16, Ramanujan matriculated at the Government College in Kumbakonam on a scholarship, but lost his scholarship the next year because he had neglected his other studies. He then failed the First Arts examination in 1906, which would have allowed him to matriculate at the University of Madras, passing math but failing his other subjects.
For the next few years, Ramanujan worked independently on mathematics, writing down results in two notebooks. In 1909, he began publishing work in the Journal of the Indian Mathematical Society, which gained him recognition for his work despite lacking a university education. Needing employment, Ramanujan became a clerk in 1912 but continued his mathematics research and gained even more recognition.
Receiving encouragement from a number of people, including the mathematician Seshu Iyer, Ramanujan sent over a letter along with about 120 mathematical theorems to G. H. Hardy, a lecturer in mathematics at Cambridge University in England. Hardy, thinking that the writer could either be a mathematician who was playing a prank or a previously undiscovered genius, asked another mathematician J.E. Littlewood, to help him look at Ramanujan’s work.
The two concluded that Ramanujan was indeed a genius. Hardy wrote back, noting that Ramanujan’s theorems fell into roughly three categories: results that were already known (or which could easily be deduced with known mathematical theorems); results that were new, and that were interesting but not necessarily important; and results that were both new and important.
Hardy immediately began to arrange for Ramanujan to come to England, but Ramanujan refused to go at first because of religious scruples about going overseas. However, his mother dreamed that the Goddess of Namakkal commanded her to not prevent Ramanujan from fulfilling his purpose. Ramanujan arrived in England in 1914 and began his collaboration with Hardy.
In 1916, Ramanujan obtained a Bachelor of Science by Research (later called a Ph.D.) from Cambridge University. His thesis was based on highly composite numbers, which are integers that have more divisors (or numbers that they can be divided by) than do integers of smaller value.
In 1917, however, Ramanujan became seriously ill, possibly from tuberculosis, and was admitted to a nursing home at Cambridge, moving to different nursing homes as he tried to regain his health.
In 1919, he showed some recovery and decided to move back to India. There, his health deteriorated again and he died there the following year.
Personal Life
On July 14, 1909, Ramanujan married Janakiammal, a girl whom his mother had selected for him. Because she was 10 at the time of marriage, Ramanujan did not live together with her until she reached puberty at the age of 12, as was common at the time.
Honors and Awards
- 1918, Fellow of the Royal Society
- 1918, Fellow of Trinity College, Cambridge University
In recognition of Ramanujan’s achievements, India also celebrates Mathematics Day on December 22, Ramanjan’s birthday.
Ramanujan died on April 26, 1920 in Kumbakonam, India, at the age of 32. His death was likely caused by an intestinal disease called hepatic amoebiasis.
Legacy and Impact
Ramanujan proposed many formulas and theorems during his lifetime. These results, which include solutions of problems that were previously considered to be unsolvable, would be investigated in more detail by other mathematicians, as Ramanujan relied more on his intuition rather than writing out mathematical proofs.
His results include:
- An infinite series for π, which calculates the number based on the summation of other numbers. Ramanujan’s infinite series serves as the basis for many algorithms used to calculate π.
- The Hardy-Ramanujan asymptotic formula, which provided a formula for calculating the partition of numbers—numbers that can be written as the sum of other numbers. For example, 5 can be written as 1 + 4, 2 + 3, or other combinations.
- The Hardy-Ramanujan number, which Ramanujan stated was the smallest number that can be expressed as the sum of cubed numbers in two different ways. Mathematically, 1729 = 1 3 + 12 3 = 9 3 + 10 3 . Ramanujan did not actually discover this result, which was actually published by the French mathematician Frénicle de Bessy in 1657. However, Ramanujan made the number 1729 well known. 1729 is an example of a “taxicab number,” which is the smallest number that can be expressed as the sum of cubed numbers in n different ways. The name derives from a conversation between Hardy and Ramanujan, in which Ramanujan asked Hardy the number of the taxi he had arrived in. Hardy replied that it was a boring number, 1729, to which Ramanujan replied that it was actually a very interesting number for the reasons above.
- Kanigel, Robert. The Man Who Knew Infinity: A Life of the Genius Ramanujan . Scribner, 1991.
- Krishnamurthy, Mangala. “The Life and Lasting Influence of Srinivasa Ramanujan.” Science & Technology Libraries , vol. 31, 2012, pp. 230–241.
- Miller, Julius. “Srinivasa Ramanujan: A Biographical Sketch.” School Science and Mathematics , vol. 51, no. 8, Nov. 1951, pp. 637–645.
- Newman, James. “Srinivasa Ramanujan.” Scientific American , vol. 178, no. 6, June 1948, pp. 54–57.
- O'Connor, John, and Edmund Robertson. “Srinivasa Aiyangar Ramanujan.” MacTutor History of Mathematics Archive , University of St. Andrews, Scotland, June 1998, www-groups.dcs.st-and.ac.uk/history/Biographies/Ramanujan.html.
- Singh, Dharminder, et al. “Srinvasa Ramanujan's Contributions in Mathematics.” IOSR Journal of Mathematics , vol. 12, no. 3, 2016, pp. 137–139.
- “Srinivasa Aiyangar Ramanujan.” Ramanujan Museum & Math Education Centre , M.A.T Educational Trust, www.ramanujanmuseum.org/aboutramamujan.htm.
- Biography of Ada Lovelace, First Computer Programmer
- Women in Mathematics History
- Biography of Charles Babbage, Mathematician and Computer Pioneer
- Biography of Joseph Louis Lagrange, Mathematician
- Leonhard Euler, Mathematician: His Life and Work
- Biography of Humphry Davy, Prominent English Chemist
- Biography of John Napier, Scottish Mathematician
- Galileo Galilei Quotes
- Biography of Blaise Pascal, 17th Century Inventor of the Calculator
- John Napier - Napier's Bones
- Leonardo da Vinci Quotes
- Biography of Leonardo Pisano Fibonacci, Noted Italian Mathematician
- Women Inventors A to Z
- Biography of Alan Turing, Code-Breaking Computer Scientist
- The History of Ethernet
- Biography of Isaac Newton, Mathematician and Scientist
Famous Scientists
Srinivasa Ramanujan
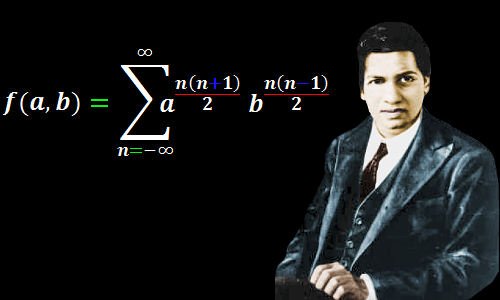
Srinivasa Ramanujan was a largely self-taught pure mathematician. Hindered by poverty and ill-health, his highly original work has considerably enriched number theory. More recently his discoveries have been applied to physics, where his theta function lies at the heart of string theory.
Srinivasa Ramanujan was born on December 22, 1887 in the town of Erode, in Tamil Nadu, in the south east of India. His father was K. Srinivasa Iyengar, an accounting clerk for a clothing merchant. His mother was Komalatammal, who earned a small amount of money each month as a singer at the local temple.
His family were Brahmins, the Hindu caste of priests and scholars. His mother ensured the boy was in tune with Brahmin traditions and culture. Although his family were high caste, they were very poor.
Ramanujan’s parents moved around a lot, and he attended a variety of different elementary schools.
Early Mathematics At age 10, Ramanujan was the top student in his district and he started high school at the Kumbakonam Town High School. Looking at the mathematics books in his school’s library, he quickly found his vocation. By age 12, he had begun serious self-study of mathematics, working through cubic equations and arithmetic and geometric series. He invented his own method of solving quartic equations.
As Ramanujan’s mathematical knowledge developed, his main source of inspiration and expertise became Synopsis of elementary results in pure mathematics by George S. Carr. This book presented a very large number of mathematical results – over 4000 theorems – but generally showed little working, cramming into its pages as many results as possible.
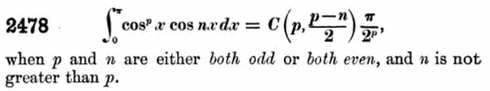
Entry 2478 from Carr’s Synopsis of elementary results in pure mathematics
With little other guidance, Ramanujan came to believe this was how mathematics was done, so he himself learned to show little working. Also, he could afford only a small amount of paper, doing most of his work on slate with chalk, transferring a minimal amount of his working and his results to paper.
His memory for mathematical formulas and constants seems to have been boundless: he amazed classmates with his ability to recite the values of irrational numbers like π, e, and √ 2 to as many decimal places as they asked for.
An Apparently Bright Future Fizzles Out In 1904, Ramanujan left high school; his future looked promising: he had won the school’s mathematics prize and, more importantly, a scholarship allowing him to study at the Government Arts College in the town of Kumbakonam.
Obsessed with mathematics, Ramanujan failed his non-mathematical exams and lost his scholarship. In 1905, he traveled to Madras and enrolled at Pachaiyappa’s College, but again failed his non-mathematical exams.
The Discovery of Ramanujan as a Mathematician of Genius
The Hungry Years At the beginning of 1907, at age 19, with minimal funds and a stomach all too often groaning with hunger, Ramanujan continued on the path he had chosen: total devotion to mathematics. The mathematics he was doing was highly original and very advanced.
Even though (or some might say because) he had very little formal mathematical education he was able to discover new theorems. He also independently discovered results originally discovered by some of the greatest mathematicians in history, such as Carl Friedrich Gauss and Leonhard Euler .
Ill-health was Ramanujan’s constant companion – as it would be for much of his short life.
By 1910, he realized he must find work to stay alive. In the city of Madras he found some students who needed mathematics tutoring and he also walked around the city offering to do accounting work for businesses.
And then a piece of luck came his way. Ramanujan tried to find work at the government revenue department, and there he met an official whose name was Ramaswamy Aiyer. Ramanujan did not have a resume to show Ramaswamy Aiyer; all he had were his notebooks – the results of his mathematical work.
Ramanujan’s good fortune was that Ramaswamy Aiyer was a mathematician. He had only recently founded the Indian Mathematical Society, and his jaw dropped when he saw Ramanujan’s work.

Things Begin to Look Up Ramaswamy Aiyer contacted the secretary of the Indian Mathematical Society, R. Ramachandra Rao, suggesting he provide financial support for Ramanujan. At first Rao resisted the idea, believing Ramanujan was simply copying the work of earlier great mathematicians. A meeting with Ramanujan, however, convinced Rao that he was dealing with a genuine mathematical genius. He agreed to provide support for Ramanujan, and Ramaswamy Aiyer began publishing Ramanujan’s work in the Journal of the Indian Mathematical Society .
Ramanujan’s work, however, was hard to understand. The style he had adopted as a schoolboy, after digesting George S. Carr’s book, contributed to the problem. His mathematics often left too few clues to allow anyone who wasn’t also a mathematical genius to see how he obtained his results.
In March 1912, his financial position improved when he got a job as an accounting clerk with the Madras Port Trust.
There he was encouraged to do mathematics at work after finishing his daily tasks by the port’s Chief Accountant, S. Narayana Iyer, who was treasurer of the Indian Mathematical Society, and by Sir Francis Spring, an engineer, who was Chairman of the Madras Port Trust.
Francis Spring began pressing for Ramanujan’s mathematical work to be supported by the government and for him to be appointed to a research position at one of the great British universities.
A Crank or a Genius? Ramanujan and his supporters contacted a number of British professors, but only one was receptive – an eminent pure mathematician at the University of Cambridge – Godfrey Harold Hardy, known to everyone as G. H. Hardy, who received a letter from Ramanujan in January 1913. By this time, Ramanujan had reached the age of 25.
Professor Hardy puzzled over the nine pages of mathematical notes Ramanujan had sent. They seemed rather incredible. Could it be that one of his colleagues was playing a trick on him?
Hardy reviewed the papers with J. E. Littlewood, another eminent Cambridge mathematician, telling Littlewood they had been written by either a crank or a genius, but he wasn’t quite sure which. After spending two and a half hours poring over the outlandishly original work, the mathematicians came to a conclusion. They were looking at the papers of a mathematical genius:

Hardy was eager for Ramanujan to move to Cambridge, but in accordance with his Brahmin beliefs, Ramanujan refused to travel overseas. Instead, an arrangement was made to fund two years of work at the University of Madras. During this time, Ramanujan’s mother had a dream in which the goddess Namagiri told her she should give her son permission to go to Cambridge, and this she did. Her decision led to several very heated quarrels with other devout family members.
Ramanujan at Cambridge
Ramanujan arrived in Cambridge in April 1914, three months before the outbreak of World War 1. Within days he had begun work with Hardy and Littlewood. Two years later, he was awarded the equivalent of a Ph.D. for his work – a mere formality.

Srinivasa Ramanujan at Cambridge
Ramanujan’s prodigious mathematical output amazed Hardy and Littlewood.
The notebooks he brought from India were filled with thousands of identities, equations, and theorems he discovered for himself in the years 1903 – 1914.
Some had been discovered by earlier mathematicians; some, through inexperience, were mistaken; many were entirely new.
Explaining Ramanujan’s Extraordinary Mathematical Output
Ramanujan had very little formal training in mathematics, and indeed large areas of mathematics were unknown to him. Yet in the areas familiar to him and in which he enjoyed working, his output of new results was phenomenal.
Ramanujan said the Hindu goddess Namagiri – who had appeared in his mother’s dream telling her to allow him to go to Cambridge – had appeared in one of his own dreams .

According to Hardy, Ramanujan’s ideas were:
It is possible that Ramanujan’s brain was wired differently from most mathematicians.
He seems to have had a personal window through which some problems in number theory appeared with a clarity denied to most people in the field. Results they fought for through days of arduous thought seemed obvious to Ramanujan.
Professor Bruce Berndt is an analytic number theorist who, since 1977, has spent decades researching Ramanujan’s theorems. He has published several books about them, establishing that the great majority are correct. He was told an interesting story by the great Hungarian mathematician Paul Erdős about something G. H. Hardy had once said to him:

Given that David Hilbert is regarded by many as the greatest mathematician of the early twentieth century, and Hardy and Littlewood were immensely influential mathematicians, it is fascinating to see how exceptional Hardy thought Ramanujan’s raw mathematical ability was.
Number Theory and String Theory In 1918 Ramanujan became the first Indian mathematician to be elected a Fellow of the British Royal Society:
“Distinguished as a pure mathematician particularly for his investigation in elliptic functions and the theory of numbers.”
In his short lifetime he produced almost 4000 proofs, identities, conjectures, and equations in pure mathematics.
His theta function lies at the heart of string theory in physics.
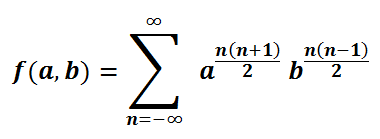
The Ramanujan theta function.

Some Personal Details and the End
In July 1909, Ramanujan married S. Janaki Ammal, who was then just 10 years old. The marriage had been arranged by Ramanujan’s mother. The couple began sharing a home in 1912.
When Ramanujan left to study at the University of Cambridge, his wife moved in with Ramanujan’s parents. Ramanujan’s scholarship was sufficient for his needs in Cambridge and the family’s needs in Kumbakonam.
For his first three years in Cambridge, Ramanujan was very happy. His health, however, had always been rather poor. The winter weather in England, much colder than anything he had ever imagined, made him ill for a time.
In 1917, he was diagnosed with tuberculosis and worryingly low vitamin levels. He spent months being cared for in sanitariums and nursing homes.
In February 1919, his health seemed to have recovered sufficiently for him to return to India, but sadly he lived for only one more year.
Srinivasa Ramanujan died aged 32 in Madras on April 26, 1920. His death was most likely caused by hepatic amoebiasis caused by liver parasites common in Madras. His body was cremated.
Sadly, some of Ramanujan’s Brahmin relatives refused to attend his funeral because he had traveled overseas.

Author of this page: The Doc Images digitally enhanced and colorized by this website. © All rights reserved.
Cite this Page
Please use the following MLA compliant citation:
Published by FamousScientists.org
Creative Commons Images Image of Paul Erdős by Topsy Kretts, Creative Commons Attribution 3.0 Unported License.
Image of Michio Kaku by Campus Party Brasil , Creative Commons Attribution-Share Alike 2.0 Generic License.
Further Reading Srinivasa Ramanujan Aiyangar, Godfrey Harold Hardy, P. Venkatesvara Seshu Aiyar, Bertram Martin Wilson Collected Papers of Srinivasa Ramanujan American Mathematical Soc., 1927
Bruce C. Berndt Ramanujan’s Notebooks Part 1 Springer Verlag, 1985
Srinivasa Ramanujan Aiyangar Ramanujan: Letters and Commentary American Mathematical Soc., 1995
Godfrey Harold Hardy Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work AMS Chelsea Pub., 1 Jan 1999
B A Kupershmidt A Review of Bruce C. Berndt’s Ramanujan’s Notebooks, Parts I – V. Journal of Nonlinear Mathematical Physics, V.7, N 2, R7–R37, 2000
More from FamousScientists.org:

Alphabetical List of Scientists
Louis Agassiz | Maria Gaetana Agnesi | Al-Battani Abu Nasr Al-Farabi | Alhazen | Jim Al-Khalili | Muhammad ibn Musa al-Khwarizmi | Mihailo Petrovic Alas | Angel Alcala | Salim Ali | Luis Alvarez | Andre Marie Ampère | Anaximander | Carl Anderson | Mary Anning | Virginia Apgar | Archimedes | Agnes Arber | Aristarchus | Aristotle | Svante Arrhenius | Oswald Avery | Amedeo Avogadro | Avicenna
Charles Babbage | Francis Bacon | Alexander Bain | John Logie Baird | Joseph Banks | Ramon Barba | John Bardeen | Charles Barkla | Ibn Battuta | William Bayliss | George Beadle | Arnold Orville Beckman | Henri Becquerel | Emil Adolf Behring | Alexander Graham Bell | Emile Berliner | Claude Bernard | Timothy John Berners-Lee | Daniel Bernoulli | Jacob Berzelius | Henry Bessemer | Hans Bethe | Homi Jehangir Bhabha | Alfred Binet | Clarence Birdseye | Kristian Birkeland | James Black | Elizabeth Blackwell | Alfred Blalock | Katharine Burr Blodgett | Franz Boas | David Bohm | Aage Bohr | Niels Bohr | Ludwig Boltzmann | Max Born | Carl Bosch | Robert Bosch | Jagadish Chandra Bose | Satyendra Nath Bose | Walther Wilhelm Georg Bothe | Robert Boyle | Lawrence Bragg | Tycho Brahe | Brahmagupta | Hennig Brand | Georg Brandt | Wernher Von Braun | J Harlen Bretz | Louis de Broglie | Alexander Brongniart | Robert Brown | Michael E. Brown | Lester R. Brown | Eduard Buchner | Linda Buck | William Buckland | Georges-Louis Leclerc, Comte de Buffon | Robert Bunsen | Luther Burbank | Jocelyn Bell Burnell | Macfarlane Burnet | Thomas Burnet
Benjamin Cabrera | Santiago Ramon y Cajal | Rachel Carson | George Washington Carver | Henry Cavendish | Anders Celsius | James Chadwick | Subrahmanyan Chandrasekhar | Erwin Chargaff | Noam Chomsky | Steven Chu | Leland Clark | John Cockcroft | Arthur Compton | Nicolaus Copernicus | Gerty Theresa Cori | Charles-Augustin de Coulomb | Jacques Cousteau | Brian Cox | Francis Crick | James Croll | Nicholas Culpeper | Marie Curie | Pierre Curie | Georges Cuvier | Adalbert Czerny
Gottlieb Daimler | John Dalton | James Dwight Dana | Charles Darwin | Humphry Davy | Peter Debye | Max Delbruck | Jean Andre Deluc | Democritus | René Descartes | Rudolf Christian Karl Diesel | Diophantus | Paul Dirac | Prokop Divis | Theodosius Dobzhansky | Frank Drake | K. Eric Drexler
John Eccles | Arthur Eddington | Thomas Edison | Paul Ehrlich | Albert Einstein | Gertrude Elion | Empedocles | Eratosthenes | Euclid | Eudoxus | Leonhard Euler
Michael Faraday | Pierre de Fermat | Enrico Fermi | Richard Feynman | Fibonacci – Leonardo of Pisa | Emil Fischer | Ronald Fisher | Alexander Fleming | John Ambrose Fleming | Howard Florey | Henry Ford | Lee De Forest | Dian Fossey | Leon Foucault | Benjamin Franklin | Rosalind Franklin | Sigmund Freud | Elizebeth Smith Friedman
Galen | Galileo Galilei | Francis Galton | Luigi Galvani | George Gamow | Martin Gardner | Carl Friedrich Gauss | Murray Gell-Mann | Sophie Germain | Willard Gibbs | William Gilbert | Sheldon Lee Glashow | Robert Goddard | Maria Goeppert-Mayer | Thomas Gold | Jane Goodall | Stephen Jay Gould | Otto von Guericke
Fritz Haber | Ernst Haeckel | Otto Hahn | Albrecht von Haller | Edmund Halley | Alister Hardy | Thomas Harriot | William Harvey | Stephen Hawking | Otto Haxel | Werner Heisenberg | Hermann von Helmholtz | Jan Baptist von Helmont | Joseph Henry | Caroline Herschel | John Herschel | William Herschel | Gustav Ludwig Hertz | Heinrich Hertz | Karl F. Herzfeld | George de Hevesy | Antony Hewish | David Hilbert | Maurice Hilleman | Hipparchus | Hippocrates | Shintaro Hirase | Dorothy Hodgkin | Robert Hooke | Frederick Gowland Hopkins | William Hopkins | Grace Murray Hopper | Frank Hornby | Jack Horner | Bernardo Houssay | Fred Hoyle | Edwin Hubble | Alexander von Humboldt | Zora Neale Hurston | James Hutton | Christiaan Huygens | Hypatia
Ernesto Illy | Jan Ingenhousz | Ernst Ising | Keisuke Ito
Mae Carol Jemison | Edward Jenner | J. Hans D. Jensen | Irene Joliot-Curie | James Prescott Joule | Percy Lavon Julian
Michio Kaku | Heike Kamerlingh Onnes | Pyotr Kapitsa | Friedrich August Kekulé | Frances Kelsey | Pearl Kendrick | Johannes Kepler | Abdul Qadeer Khan | Omar Khayyam | Alfred Kinsey | Gustav Kirchoff | Martin Klaproth | Robert Koch | Emil Kraepelin | Thomas Kuhn | Stephanie Kwolek
Joseph-Louis Lagrange | Jean-Baptiste Lamarck | Hedy Lamarr | Edwin Herbert Land | Karl Landsteiner | Pierre-Simon Laplace | Max von Laue | Antoine Lavoisier | Ernest Lawrence | Henrietta Leavitt | Antonie van Leeuwenhoek | Inge Lehmann | Gottfried Leibniz | Georges Lemaître | Leonardo da Vinci | Niccolo Leoniceno | Aldo Leopold | Rita Levi-Montalcini | Claude Levi-Strauss | Willard Frank Libby | Justus von Liebig | Carolus Linnaeus | Joseph Lister | John Locke | Hendrik Antoon Lorentz | Konrad Lorenz | Ada Lovelace | Percival Lowell | Lucretius | Charles Lyell | Trofim Lysenko
Ernst Mach | Marcello Malpighi | Jane Marcet | Guglielmo Marconi | Lynn Margulis | Barry Marshall | Polly Matzinger | Matthew Maury | James Clerk Maxwell | Ernst Mayr | Barbara McClintock | Lise Meitner | Gregor Mendel | Dmitri Mendeleev | Franz Mesmer | Antonio Meucci | John Michell | Albert Abraham Michelson | Thomas Midgeley Jr. | Milutin Milankovic | Maria Mitchell | Mario Molina | Thomas Hunt Morgan | Samuel Morse | Henry Moseley
Ukichiro Nakaya | John Napier | Giulio Natta | John Needham | John von Neumann | Thomas Newcomen | Isaac Newton | Charles Nicolle | Florence Nightingale | Tim Noakes | Alfred Nobel | Emmy Noether | Christiane Nusslein-Volhard | Bill Nye
Hans Christian Oersted | Georg Ohm | J. Robert Oppenheimer | Wilhelm Ostwald | William Oughtred
Blaise Pascal | Louis Pasteur | Wolfgang Ernst Pauli | Linus Pauling | Randy Pausch | Ivan Pavlov | Cecilia Payne-Gaposchkin | Wilder Penfield | Marguerite Perey | William Perkin | John Philoponus | Jean Piaget | Philippe Pinel | Max Planck | Pliny the Elder | Henri Poincaré | Karl Popper | Beatrix Potter | Joseph Priestley | Proclus | Claudius Ptolemy | Pythagoras
Adolphe Quetelet | Harriet Quimby | Thabit ibn Qurra
C. V. Raman | Srinivasa Ramanujan | William Ramsay | John Ray | Prafulla Chandra Ray | Francesco Redi | Sally Ride | Bernhard Riemann | Wilhelm Röntgen | Hermann Rorschach | Ronald Ross | Ibn Rushd | Ernest Rutherford
Carl Sagan | Abdus Salam | Jonas Salk | Frederick Sanger | Alberto Santos-Dumont | Walter Schottky | Erwin Schrödinger | Theodor Schwann | Glenn Seaborg | Hans Selye | Charles Sherrington | Gene Shoemaker | Ernst Werner von Siemens | George Gaylord Simpson | B. F. Skinner | William Smith | Frederick Soddy | Mary Somerville | Arnold Sommerfeld | Hermann Staudinger | Nicolas Steno | Nettie Stevens | William John Swainson | Leo Szilard
Niccolo Tartaglia | Edward Teller | Nikola Tesla | Thales of Miletus | Theon of Alexandria | Benjamin Thompson | J. J. Thomson | William Thomson | Henry David Thoreau | Kip S. Thorne | Clyde Tombaugh | Susumu Tonegawa | Evangelista Torricelli | Charles Townes | Youyou Tu | Alan Turing | Neil deGrasse Tyson
Harold Urey
Craig Venter | Vladimir Vernadsky | Andreas Vesalius | Rudolf Virchow | Artturi Virtanen | Alessandro Volta
Selman Waksman | George Wald | Alfred Russel Wallace | John Wallis | Ernest Walton | James Watson | James Watt | Alfred Wegener | John Archibald Wheeler | Maurice Wilkins | Thomas Willis | E. O. Wilson | Sven Wingqvist | Sergei Winogradsky | Carl Woese | Friedrich Wöhler | Wilbur and Orville Wright | Wilhelm Wundt
Chen-Ning Yang
Ahmed Zewail
- Srinivasa Ramanujan
| Dec 22, 1887, in Erode, Madras Presidency (now Tamil Nadu) |
| April 26, 1920 (at age 32) in Chetput, Madras, Madras Presidency (now Tamil Nadu) |
| Indian |
| Landau–Ramanujan constant |
Srinivasa Ramanujan was a famous Indian mathematician . In a lifespan of 32 years, Ramanujan contributed more to mathematics than many other accomplished mathematicians. English mathematician G. H. Hardy, who worked with him for a number of years, described him as a natural mathematical genius. Although he had no formal training in mathematics, he made significant contributions to mathematical analysis, infinite series, continued fractions and the number theory.
Ramanujan’s Early Life
Ramanujan was born on December 22, 1887, in the town of Erode in the South Indian state of Tamilnadu. He was born in an orthodox Hindu Brahmin family. His father’s name was K Srinivasa Iyengar and his mother was Komalatammal.
Even at a young age of 10, when mathematics was first introduced to him, Ramanujan had tremendous natural ability. He mastered trigonometry by the time he was 12 years old and developed theorems on his own. By the age of 17, he was conducting his own research in fields such as Bernoulli numbers and the Euler-Mascheroni constant.
Ramanujan’s Education
Ramanujan was a brilliant student, but his obsession with mathematics took a toll on the other subjects and he had to drop out of college as he was unable to get through his college examinations.
When he was 16 years old, he got a book entitled A Synopsis of Elementary Results in Pure and Applied Mathematics , which turned his life around. The book was just a compilation of thousands of mathematical facts, published mainly as a study aid for students. The book fascinated Ramanujan and he started working with the mathematical results given in it.
With no job and coming from a poor family, life was tough for him and he had to seek the help of friends to support himself while he worked on his mathematical discoveries and tried to get it noticed from accomplished mathematicians. Eventually an Indian mathematician, Ramachandra Rao, helped him get the post of a clerk at the Madras Port Trust.
Ramanujan Breaks into Mathematics
His life changed for the better in 1913 when he wrote to G. H. Hardy, an English mathematician. As a mathematician, Hardy was used to receiving prank letters from people claiming to have discovered something new in the field. Something about Ramanujan’s letter made him take a closer look and he and J. E. Littlewood, his collaborator, concluded that this one was different. The letter contained 120 statements on theorems related to the infinite series, improper integrals, continued fractions and the number theory.
Hardy wrote back to Ramanujan and his acknowledgement changed everything for the young mathematician. He became a research scholar at the University of Madras earning almost double what his job as a clerk was paying him. However, Hardy wanted him to come over to England.
Ramanujan’s Research
Ramanujan worked with Hardy for five years. Hardy was astonished by the genius of the young mathematician and said that he had never met anyone like him. His years at England were very decisive. He gained recognition and fame. Cambridge University gave him a Bachelor of Science degree just for his research in 1916 and he was elected a Fellow of the Royal Society in 1918.
Death and Legacy
Being a strict vegetarian and a religious person himself, the cultural differences and climatic conditions took a toll on his health. In 1917, he was hospitalized in a serious condition. His health improved in 1918 and he returned to India in 1919. However, his health problems got worse again and he died on April 26, 1920, in Chennai.
Ramanujan did not offer any proof for most of his mathematical results, but other mathematicians have validated and proved many of them. Some were known earlier and a few were found to be wrong, but the vast majority have been tested and shown to be correct.
Famous Mathematicians
- Ada Lovelace
- Alan Turing
- Albert Einstein
- Andrew Wiles
- Benjamin Banneker
- Blaise Pascal
- Daniel Bernoulli
- David Hilbert
- Edward Witten
- Emmy Noether
- Eratosthenes
- Evariste Galois
- George Boole
- Georg Cantor
- Gottfried Leibniz
- Isaac Newton
- John Forbes Nash, Jr.
- John Napier
- John Von Neumann
- Leonardo Pisano Bigollo
- Luca Pacioli
- Omar Khayyám
- Pierre de Fermat
- René Descartes
- Sophie Germain
Copyright © 2013 · Famous Mathematicians · All Rights Reserved. | Disclaimer | Privacy Policy
Reset password New user? Sign up
Existing user? Log in
Srinivasa Ramanujan
Already have an account? Log in here.
Srinivasa Ramanujan (1887-1920) was an Indian mathematician who made great and original contributions to many mathematical fields, including complex analysis , number theory , infinite series , and continued fractions . He was "discovered" by G. H. Hardy and J. E. Littlewood, two world-class mathematicians at Cambridge, and enjoyed an extremely fruitful period of collaboration with them from 1914 to 1919. Unfortunately, his mathematical career was curtailed by health problems; he returned to India and died when he was only 32 years old.
Hardy, who was a great mathematician in his own right, recognized Ramanujan's genius from a series of letters that Ramanujan sent to mathematicians at Cambridge in 1913. Like much of his writing, the letters contained a dizzying array of unique and difficult results, stated without much explanation or proof. The contrast between Hardy, who was above all concerned with mathematical rigor and purity, and Ramanujan, whose writing was difficult to read and peppered with mistakes but bespoke an almost supernatural insight, produced a rich partnership.
Since his death, Ramanujan's writings (many contained in his famous notebooks) have been studied extensively. Some of his conjectures and assertions have led to the creation of new fields of study. Some of his formulas are believed to be true but as yet unproven.
There are many existing biographies of Ramanujan. The Man Who Knew Infinity , by Robert Kanigel, is an accessible and well-researched historical account of his life. The rest of this wiki will give a brief and light summary of the mathematical life of Ramanujan. As an appetizer, here is an anecdote from Kanigel's book.
In 1914, Ramanujan's friend P. C. Mahalanobis gave him a problem he had read in the English magazine Strand . The problem was to determine the number \( x \) of a particular house on a street where the houses were numbered \( 1,2,3,\ldots,n \). The house with number \( x \) had the property that the sum of the house numbers to the left of it equaled the sum of the house numbers to the right of it. The problem specified that \( 50 < n < 500 \).
Ramanujan quickly dictated a continued fraction for Mahalanobis to write down. The numerators and denominators of the convergents to that continued fraction gave all solutions \( (n,x) \) to the problem \((\)not just the particular one where \( 50 < n < 500). \) Mahalanobis was astonished, and asked Ramanujan how he had found the solution.
Ramanujan responded, "...It was clear that the solution should obviously be a continued fraction; I then thought, which continued fraction? And the answer came to my mind."
This is not the most illuminating answer! If we cannot duplicate the genius of Ramanujan, let us at least find the solution to the original problem. What is \( x \)?
\(\) Bonus: Which continued fraction did Ramanujan give Mahalanobis?
This anecdote and problem is taken from The Man Who Knew Infinity , a biography of Ramanujan by Robert Kanigel.
Taxicab numbers, nested radicals and continued fractions, ramanujan primes, ramanujan sums, the ramanujan \( \tau \) function and ramanujan's conjecture.
Many of Ramanujan's mathematical formulas are difficult to understand, let alone prove. For instance, an identity such as
\[\frac1{\pi} = \frac{2\sqrt{2}}{9801}\sum_{k=0}^{\infty} \frac{(4k)!(1103+26390k)}{(k!)^4 396^{4k}}\]
is not particularly easy to get a handle on. Perhaps this is why the most famous mathematical fact about Ramanujan is trivial and uninteresting, compared to the many brilliant theorems he proved.
The story goes that Hardy was visiting Ramanujan in the hospital, and remarked offhandedly that the taxi he had taken had a "dull number," 1729. Instantly Ramanujan replied, "No, it is a very interesting number! It is the smallest positive integer expressible as the sum of two positive cubes in two different ways."
That is, \( 1729 = 1^3+12^3 = 9^3+10^3 \).
Hardy and Wright proved in 1938 that for every \( n \), there is a positive integer \( \text{Ta}(n) \) that is expressible as the sum of two positive cubes in \( n \) different ways. So \( \text{Ta}(2) = 1729 \). \((\)The value of \( \text{Ta}(2) \) had been known since the \(17^\text{th}\) century, which is in some sense characteristic of Ramanujan as well: as he was largely self-taught, he was often rediscovering theorems that were already well-known at the same time as he was constructing entirely new ones.\()\) The numbers \( \text{Ta}(n) \) are called taxicab numbers in honor of Hardy and Ramanujan.
Ramanujan developed several formulas that allowed him to evaluate nested radicals such as \[ 3 = \sqrt{1+2\sqrt{1+3\sqrt{1+4\sqrt{\cdots}}}}. \] This is a special case of a result from his notebooks, which is proved in the wiki on nested functions .
He also contributed greatly to the theory of continued fractions . One of the identities in his letter to Hardy was \[ 1+\frac{e^{-2\pi}}{1+\frac{e^{-4\pi}}{1+\frac{e^{-6\pi}}{\cdots}}} = \left( \sqrt{\frac{5+\sqrt{5}}2} - \frac{1+\sqrt{5}}2 \right)e^{2\pi/5}. \] This and several others along these lines were among the results that convinced Hardy that Ramanujan was a brilliant mathematician. This result is in fact a special case of the Rogers-Ramanujan continued fraction , which is of the form \[ R(q) = \frac{q^{1/5}}{1+\frac{q}{1+\frac{q^2}{1+\frac{q^3}{\cdots}}}} \] and is related to the theory of modular forms, a deep branch of modern number theory.
Ramanujan's work with modular forms produced the following celebrated divisibility results involving the partition function \( p(n) \): \[ \begin{align} p(5k+4) &\equiv 0 \pmod 5 \\ p(7k+5) &\equiv 0 \pmod 7 \\ p(11k+6) &\equiv 0 \pmod{11}. \end{align} \] Ramanujan commented in the paper in which he proved these results that there did not appear to be any other simple results of the same type. But in fact there are similar congruences of the form \( p(ak+b) \equiv 0 \pmod n \) for any \( n \) relatively prime to \( 6\); this is due to Ken Ono (2000). (Even for small \( n\), the values of \( a \) and \( b \) in the congruences are quite large.) The topic remains the subject of much contemporary research.
Ramanujan proved a generalization of Bertrand's postulate , as follows: Let \( \pi(x) \) be the number of positive prime numbers \( \le x \); then for every positive integer \( n \), there exists a prime number \( R_n \) such that \[ \pi(x)-\pi(x/2) \ge n \text{ for all } x \ge R_n. \] \((\)The case \( n = 1 \), \( R_n = 2 \) is Bertrand's postulate.\()\)
The \( R_n \) are called Ramanujan primes .
The sum \( c_q(n) \) of the \(n^\text{th}\) powers of the primitive \( q^\text{th}\) roots of unity is called a Ramanujan sum . It can be shown that these are multiplicative arithmetic functions , and in fact that \[c_q(n) = \frac{\mu\left(\frac qd\right)\phi(q)}{\phi\left(\frac qd\right)},\] where \( d = \text{gcd}(q,n)\), and \( \mu \) and \( \phi \) are the Mobius function and Euler's totient function , respectively.
Let \(c_{2015}(n)\) be the sum of the \(n^\text{th}\) powers of all the primitive \(2015^\text{th}\) roots of unity, \(\omega.\) Find the minimal value of \(c_{2015}(n)\) for all positive integers \(n\).
This year's problem
Ramanujan found nice infinite sums of the form \( \sum a_n c_q(n) \) or \( \sum a_q c_q(n) \) representing the standard arithmetic functions that are important in number theory. For instance, \[ d(n) = -\frac1{2\gamma+\ln(n)} \sum_{q=1}^{\infty} \frac{\ln(q)^2}{q} c_q(n), \] where \( \gamma \) is the Euler-Mascheroni constant .
Another example: the identity \[ \sum_{q=1}^{\infty} \frac{c_q(n)}{q} = 0 \] turns out to be equivalent to the prime number theorem .
Sums involving \( c_q(n) \) are known as Ramanujan sums ; these were also used in applications including the proof of Vinogradov's theorem that every sufficiently large odd positive integer is the sum of three primes.
Ramanujan's \( \tau \) function is defined by the formula \[ \sum_{n=1}^{\infty} \tau(n) q^n = q\prod_{n=1}^{\infty} (1-q^n)^{24} \] and is related to the theory of modular forms.
Ramanujan conjectured several properties of the \( \tau \) function, including \[ |\tau(p)| \le 2p^{11/2} \text{ for all primes } p. \] This turned out to be an extremely important and deep result, which was proved in 1974 by Pierre Deligne in his Fields-medal-winning proofs of the Weil conjectures on points on algebraic varieties over finite fields.
Problem Loading...
Note Loading...
Set Loading...
Famous Mathematicians
List and Biographies of Great Mathematicians
Srinivasa Ramanujan

Srinivasa Ramanujan was born on December 22, 1887 in Erode, a city in the Tamil Nadu state of India. His father, K. Srinivasa Iyengar was a clerk while his mother, Komalatammal performed as a singer, in a temple. Even though they belonged to the Brahmins who are known to be the highest caste of Hinduism, Ramanujan’s family was very poor.
At the age of 10, in 1897, Ramanujan attended the high school in Kumbakonam Town. There he discovered his intelligence in the field of mathematics and by his independent study of books from the school library; Ramanujan increased his knowledge and skills. At age of just 12 years, he had developed understanding of trigonometry and was able to solve cubic equations and arithmetic and geometric series as well.
Among all of the mathematical literature Ramanujan went through, a book by George Shoobridge Carr , titled as A Synopsis of Elementary Results in Pure and Applied Mathematics , written in 1886, proved to be the primary medium that laid him onto the path of becoming a great mathematician. He got access to its copy in 1902 and in a short time he not only went through all of its theorems but also verified their results. He also rediscovered the work done by many famous mathematicians including Carl Friedrich Gauss and Leonhard Euler . In addition to this, many new theorems were also formulated by him.
Ramanujan completed his high school by the age of 17, in 1904. Due to his outstanding results, he was awarded scholarship for higher studies in the Government Arts College in Kumbakonam. But his inclination towards mathematics led to his failure in non-mathematical subjects and ultimately discontinuation of his scholarship. Ramanujan had to face the same situation in Pachaiyappa’s College, an affiliation of the University of Madras by losing his scholarship there.
When Ramanujan got married at the age of 22, in 1909, he got worried for his financial instability, but was still strong-willed to continue with his passion. He started independent research work in mathematics by getting enrolled in a college. He was supported by a government official and secretary of the Indian Mathematical Society , Ramachandra Rao .
In 1911, Ramanujan got his first publication with the assistance of Ramaswamy Aiyer , the founder of the Indian Mathematical Society , in the society’s journal only. This research was on Bernoulli Numbers , done independently by him in 1904. After about a year, Ramanujan started working in Madras at the Port Trust Office as a clerk alongside his research work.
After applying for British Universities in 1913, Ramanujan’s work got acknowledged by a prominent mathematician of the Cambridge University , Godfrey Harold Hardy who funded him for research in the University of Madras. In 1914, Ramanujan went to England to utilize his scholarship at Trinity College, Cambridge and work in collaboration with G. H. Hardy and J. E. Littlewood . In 1916, Ramanujan got his Bachelors in Science degree and a year later he became a fellow of the British Royal Society .
Ramanujan has contributed a lot to mathematics in his short lifespan. This includes his independent works from India as well as the researches done under the mentorship of G. H. Hardy in England. Alongside his outstanding discoveries in continued fractions , divergent series , hypergeometric series , Reimann series and elliptic integrals , his advancements in partition of numbers are quite phenomenal. Ramanujan worked on properties of partition function and in collaboration with G. H. Hardy, developed the circular method to represent an integer in the form of its partitions. This led to many developments in analytic number theory by future mathematicians.
In 1917, Ramanujan got diagnosed with tuberculosis. He returned to India in 1919 and died in 1920, at the age of 32.
About three months before his death, Ramanujan wrote his last letter to Hardy, explaining his new discovery in mathematics; the Theta Function and its 17 identities. Later, many mathematicians worked on this function, proved the identities and found new ones too.
Even though Ramanujan had got many papers published in different journals during his life, much work remained unpublished. The notes that he left behind were studied by many mathematicians after him, who verified his discoveries, and found their potential applications.
- School guide
- Social Science Notes
- History Notes
- Geography Notes
- Political Science Notes
- Economics Notes
- Science and Technology Notes
- Social Science Solutions
- English Grammar
- Science Solution
- Biology Solutions
- Mathematics Solutions
- R.D.Sharma Solutions
Srinivasa Ramanujan Biography: Education, Contribution, Interesting Facts
Srinivasa Ramanujan: Srinivasa Ramanujan (1887–1920) was an Indian mathematician known for his brilliant, self-taught contributions to number theory and mathematical analysis. His work, including discoveries in infinite series and modular forms, has had a lasting impact on mathematics.
In this article, We have covered the Complete Biography of Srinivasa Ramanujan including his early childhood and education, Srinivasa Ramanujan’s Contribution to Mathematics, Interesting Facts about him, and many more.
Let’s dive right in.

Srinivasa Ramanujan Biography
Table of Content
Srinivasa Ramanujan Biography Overview
Srinivasa ramanujan early life and education, srinivasa ramanujan in england, srinivasa ramanujan contribution to mathematics, srinivasa ramanujan discovery, interesting facts about srinivasa ramanujan, awards and achievements of srinivasa ramanujan.
Here are some major details about Srinivasa Ramanujan FRS as mentioned below:
| Full Name | Srinivasa Ramanujan FRS (Fellow of the Royal Society) |
|---|---|
| Father | Kuppuswamy Srinivasa Iyengar. |
| Mother | Komalatamma. |
| Born | 22nd December, 1887. |
| Birth Place | Erode, Madras Presidency (now Tamil Nadu), India. |
| Died | 26th April, 1920. |
| Cause Of Death | Tuberculosis. |
| Death Place | Kumbakonam, Madras Presidency, British India. |
| Field Of Work | Mathematics. |
| Contributions In Mathematics | Mathematical analysis, number theory, infinite series, continued fractions, modular forms and mock theta functions. |
| Education | He was a self-taught mathematician with no formal education in mathematics. |
| Recognitions | He was the Fellow of the Royal Society in 1918. He was awarded the Bôcher Memorial Prize in 1921 (Posthumously). |
Srinivasa Ramanujan FRS was an Indian mathematician who was the mathematics god in contemporary times. The genius proposed some theories and works in the 20th century that are still relevant in this 21st century.
Birth of Srinivasa Ramanujan
Srinivasa Ramanujan was born on December 22, 1887, in Erode, India. A self-taught mathematician, he made significant contributions to number theory and mathematical analysis, despite facing limited formal education.He was born in a poor family. His father was a clerk. His mother was a homemaker.
He was born on 22nd December 1887. His native place is a south Indian town of Tamil Nadu, named Erode. His father Mr. Kuppuswamy Srinivasa Iyengar worked as a clerk in a saree shop. His mother Mrs. Komalatamma was a housewife.
Education of Srinivasa Ramanujan
Srinivasa Ramanujan did his early schooling in Madras. He was a self taught mathematician. He won so many academic prizes in his high school. In his college life started to study mathematics only. He performed bad in all other subjects. He dropped out of college due to the academic reasons. His theories got a final breakdown at this stage.
His early education was started in Madras. He fall in love with Mathematics at a very young age. He got many academis prizes in his school life. He continued to study one subject in collge and kept failing in other subjects. For this he became a dropped out student.
Final Breakthrough in life of Srinivasa Ramanujan
At this time Ramanujan sent his works to the International mathematicians. In 1912, he was working as a clerk in the Madras Post Trust Office. At this time he reached out to the famous mathematician G.H. Hardy. In 1913, he sent his 120 theorems to the famous mathematician G.H. Hardy. G.H. Hardy analysed his work and from here Ramanujan became a genius for the world. He moved to abroad to work more on these theories.
After dropping out from college, he started to send his work to International mathematicians. In 1912, he was appointed as a clerk of Madras Post Trust Office. The manager of Madras Post Trust Office, SN Aiyar helped him to communicate with G.H. Hardy.
Srinivasa Ramanujan’s time in England, particularly at Cambridge University, was a crucial period in his life marked by significant mathematical contributions, collaboration. Here is his time in England chronologically.
- 1914: Ramanujan arrived in England in April 1914, initially facing challenges in adapting to the climate and culture.
- Collaboration with G. H. Hardy: Upon his arrival, he started collaborating with G. H. Hardy at Cambridge University. Hardy recognized Ramanujan’s exceptional talent and the two worked closely on various mathematical problems.
- 1916: Despite lacking formal academic credentials, Ramanujan was admitted to Cambridge University based on the strength of his mathematical work. He became a research student.
- Contributions to Mathematics: Between 1914 and 1919, Ramanujan produced over 30 research papers, making profound contributions to number theory, modular forms, and elliptic functions, among other areas.
- Recognition and Fellowships: In 1918, Ramanujan was elected a Fellow of the Royal Society, a prestigious recognition of his outstanding contributions to mathematics.
- Health Challenges: Ramanujan faced health challenges during his time in England, exacerbated by malnutrition. His dedication to mathematics often led him to neglect his well-being.
- Return to India: Due to deteriorating health, Ramanujan returned to India in 1919. His contributions to mathematics during his time in England left an indelible mark on the field.
Here are some major contributions of Srinivasa Ramanujan as mentioned below:
- Developed advanced formulas for hypergeometric series and discovered relationships between different series.
- Contributed to the theory of q-series and modular forms.
- Identified the famous number 1729 as the smallest positive integer expressible as the sum of two cubes in two distinct ways.
- Introduced and studied mock theta functions, extending the theory of theta functions in modular forms.
- Investigated the partition function, yielding groundbreaking results and congruences that significantly advanced number theory.
- Proposed the concept of the Ramanujan prime, contributing to the understanding of prime numbers.
- Worked on the tau function, providing insights into modular forms and elliptic functions.
- Made profound contributions to the theory of theta functions and elliptic functions, impacting the field of complex analysis.
- Strived to unify different areas of mathematics, demonstrating a deep understanding of mathematical structures.
- Collaborated with G. H. Hardy at Cambridge University, resulting in joint publications that enriched the field of mathematics.
- Developed theorems in calculus, showcasing his ability to provide rigorous mathematical proofs for his intuitive results.
The following are some of the some of the notable discoveries of Srinivasa Ramanujan:
| Developed numerous formulas for infinite series, including results related to hypergeometric series. | |
| Identified 1729 as the smallest positive integer expressible as the sum of two cubes in two ways. | |
| Introduced mock theta functions, expanding the theory of modular forms and number theory. | |
| Explored the partition function, discovering congruences that significantly impacted number theory. | |
| Introduced the concept of the Ramanujan prime and contributed to the tau function in modular forms. | |
| Advanced the study of theta functions and elliptic functions, deepening the understanding of these mathematical concepts. | |
| Worked towards unifying different mathematical theories, showcasing a holistic approach. | |
| Collaborated with G. H. Hardy, resulting in joint publications and advancements in mathematical research. |
People Also View:
- Who is the Father of Indian Mathematics?
- Who Invented Zero? – Explanation and FAQs
- Who is the Father of Arithmetic?
- Who discovered whole numbers?
- Ramanujan had no formal training in mathematics and was largely self-taught. His early exposure to advanced mathematical concepts was through books he obtained and studied on his own.
- Ramanujan was known for his intuitive approach to mathematics. He often presented results without formal proofs, and many of his theorems were later proven by other mathematicians.
- By the age of 13, Ramanujan had independently developed theorems in advanced trigonometry and infinite series. His mathematical talent was evident from a young age.
- As a child, Ramanujan discovered the formula for the sum of an infinite geometric series at the age of 14, which was published in the Journal of the Indian Mathematical Society.
- During a visit to Ramanujan in the hospital, G. H. Hardy mentioned taking a rather dull taxi with the number 1729. Ramanujan immediately replied that 1729 is an interesting number as it is the smallest number that can be expressed as the sum of two cubes in two different ways: 1729=13+123=93+1031729=13+123=93+103. This incident led to the term “taxicab number.”
- Ramanujan made substantial contributions to number theory, particularly in the areas of prime numbers, modular forms, and elliptic functions.
- In 1918, Ramanujan was elected a Fellow of the Royal Society, a prestigious recognition of his outstanding contributions to mathematics.
- Ramanujan faced health issues during his time in England, partly due to nutritional deficiencies. His dedication to mathematics sometimes led him to neglect his well-being.
Srinivasa Ramanujan FRS was a briliant personality from his childhood. He achieved so many things in his 35 years of life. Here is his Awards and Achievements given below.
| 1918 | Fellow of the Royal Society |
| 1917 | Adams Prize |
| 1920 | Honorary Doctorate from the University of Cambridge |
He had completely read Loney’s book on Plane trigimetry at the age of 12.
- He became the first Indian to be honored as a Fellow of the Royal Society.
- In 1997, The Ramanujan Journal was launched to publish about his work.
- 2012 was declared as the National Mathematical Year in India.
- Since 2021 in India, his birth anniversary has been observed as the National Mathematicians Day every year.
- Famous Scientists and Their Inventions
- List of Physics Scientists and Their Inventions
- Top 10 Isaac Newton Inventions & Revolutionary Discoveries
FAQs on Srinivasa Ramanujan Biography
What is the meaning of frs in srinivasa ramanujan.
The meaning of FRS is Fellow of Royal Society.
When did Ramanujan got FRS?
On 2nd May 1918 Ramanujan got FRS .
Why is 1729 called Ramanujan number?
1729 as the sum of two positive cubes. It is known as the Hardy–Ramanujan number.
What is Ramanujan famous for?
Ramanujan’s contribution extends to mathematical fields such as complex analysis, number theory, infinite series, and continued fractions.
Why did Ramanujan died at 32?
At the age of 32 Ramanujan died due to tuberculosis.
What was the invention of Srinivasa Ramanujan?
Srinivasa Ramanujan made groundbreaking contributions to mathematics, discovering formulas for infinite series, introducing concepts like modular forms and mock theta functions, and making significant advancements in number theory. His work has had a lasting impact on diverse mathematical fields.
Who was the wife of Srinivasa Ramanujan?
Srinivasa Ramanujan’s wife was Janaki Ammal. They got married in July 1909 when Ramanujan was 21 years old, and Janaki was 10 years old. Their marriage was arranged, following the customs of the time in India.
Did Srinivasa Ramanujan have Child?
Yes, Srinivasa Ramanujan and his wife Janaki Ammal had a son named Namagiri Thayar. The couple named their son after the goddess Namagiri Thayar, to whom Ramanujan attributed the inspiration for some of his mathematical insights.

Please Login to comment...
Similar reads.
- School History
- School Learning
- Social Science
Improve your Coding Skills with Practice
What kind of Experience do you want to share?
Srinivasa Ramanujan Biography
Birthday: December 22 , 1887 ( Capricorn )
Born In: Erode

Recommended For You

Indian Celebrities Born In December
Died At Age: 32
Spouse/Ex-: Janaki Ammal
father: K. Srinivasa Iyengar
mother: Komalat Ammal
siblings: Sadagopan Ramanujan
Born Country: India
Poorly Educated Mathematicians
Died on: April 26 , 1920
place of death: Kumbakonam, Madras Presidency, British India
Cause of Death: Amoebiasis
education: Government Arts College, Pachaiyappa's College, Trinity College, Cambridge (BSc, 1916)
awards: ICTP Ramanujan Prize SASTRA Ramanujan Prize
You wanted to know
What is srinivasa ramanujan known for.
Srinivasa Ramanujan is known for his significant contributions to mathematical analysis, number theory, infinite series, and continued fractions.
What is Ramanujan's famous mathematical formula?
Ramanujan is famous for his formula for the partition function, which gives the number of ways a number can be expressed as a sum of positive integers.
What is the Ramanujan conjecture?
The Ramanujan conjecture is a famous unsolved problem in mathematics related to the properties of certain arithmetic functions.
How did Ramanujan independently discover new mathematical results?
Ramanujan often stated that his mathematical ideas came to him as visions from a Hindu goddess, inspiring his groundbreaking work.
Recommended Lists:
See the events in life of Srinivasa Ramanujan in Chronological Order

How To Cite
People Also Viewed

Also Listed In
© Famous People All Rights Reserved
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||















































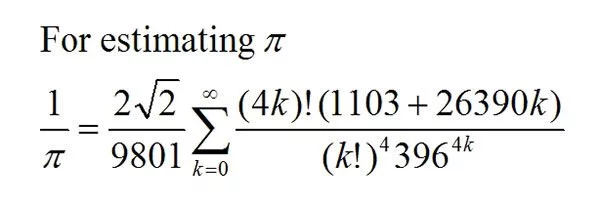

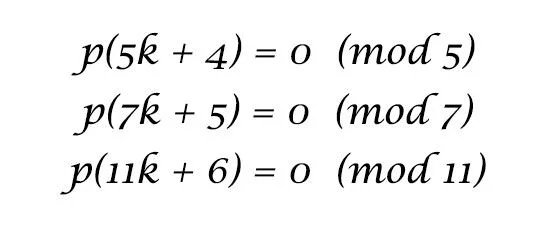






















IMAGES
COMMENTS
Srinivasa Ramanujan (born December 22, 1887, Erode, India—died April 26, 1920, Kumbakonam) was an Indian mathematician whose contributions to the theory of numbers include pioneering discoveries of the properties of the partition function.. When he was 15 years old, he obtained a copy of George Shoobridge Carr's Synopsis of Elementary Results in Pure and Applied Mathematics, 2 vol. (1880 ...
Srinivasa Ramanujan [a] (22 December 1887 - 26 April 1920) was an Indian mathematician.Though he had almost no formal training in pure mathematics, he made substantial contributions to mathematical analysis, number theory, infinite series, and continued fractions, including solutions to mathematical problems then considered unsolvable.. Ramanujan initially developed his own mathematical ...
Birth -. Srinivasa Ramanujan was born on 22nd December 1887 in the south Indian town of Tamil Nad, named Erode. His father, Kuppuswamy Srinivasa Iyengar worked as a clerk in a saree shop and his mother, Komalatamma was a housewife. Since a very early age, he had a keen interest in mathematics and had already become a child prodigy.
Srinivasa Ramanujan was born on December 22, 1887, in Erode, India, a small village in the southern part of the country. Shortly after this birth, his family moved to Kumbakonam, where his father ...
Biography. Srinivasa Ramanujan was one of India's greatest mathematical geniuses. He made substantial contributions to the analytical theory of numbers and worked on elliptic functions, continued fractions, and infinite series. Ramanujan was born in his grandmother's house in Erode, a small village about 400 km southwest of Madras (now Chennai).
Ramanujan was born on December 22, 1887, in Erode, a city in southern India. His father, K. Srinivasa Aiyangar, was an accountant, and his mother Komalatammal was the daughter of a city official. Though Ramanujan's family was of the Brahmin caste, the highest social class in India, they lived in poverty. Ramanujan began attending school at ...
Lived 1887 - 1920. Srinivasa Ramanujan was a largely self-taught pure mathematician. Hindered by poverty and ill-health, his highly original work has considerably enriched number theory. More recently his discoveries have been applied to physics, where his theta function lies at the heart of string theory. Advertisements Beginnings Srinivasa Ramanujan was born on December 22,
Ramanujan was born on December 22, 1887, in the town of Erode in the South Indian state of Tamilnadu. He was born in an orthodox Hindu Brahmin family. His father's name was K Srinivasa Iyengar and his mother was Komalatammal. Even at a young age of 10, when mathematics was first introduced to him, Ramanujan had tremendous natural ability.
Srinivasa Ramanujan (1887-1920) was an Indian mathematician who made great and original contributions to many mathematical fields, including complex analysis, number theory, infinite series, and continued fractions. He was "discovered" by G. H. Hardy and J. E. Littlewood, two world-class mathematicians at Cambridge, and enjoyed an extremely fruitful period of collaboration with them ...
Srinivasa Ramanujan was born on December 22, 1887 in Erode, a city in the Tamil Nadu state of India. His father, K. Srinivasa Iyengar was a clerk while his mother, Komalatammal performed as a singer, in a temple. Even though they belonged to the Brahmins who are known to be the highest caste of Hinduism, Ramanujan's family was very poor. At ...
The Hardy-Ramanujan Number (1729): During a visit to Ramanujan in the hospital, G. H. Hardy mentioned taking a rather dull taxi with the number 1729. Ramanujan immediately replied that 1729 is an interesting number as it is the smallest number that can be expressed as the sum of two cubes in two different ways: 1729=13+123=93+1031729=13+123=93+103.
Srinivasa Ramanujan was born on December 22, 1887 in his grandmother's house in a small village called Erode. Erode is around 400 km from Chennai, the capital of the Indian state of Tamil Nadu. Ramanujan's father, Kuppuswamy Srinivasa Iyengar, was a clerk in a cloth merchant's shop; while his mother, Komalatammal, was a housewife and sang ...
Childhood & Early Life. Srinivasa Ramanujan was born on 22 December 1887, in Erode, Madras Presidency, British India, to K. Srinivasa Iyengar and his wife Komalatammal. His family was a humble one and his father worked as a clerk in a sari shop. His mother gave birth to several children after Ramanujan, but none survived infancy.
Ramanujan, Srinivasa (1887-1920) Indian mathematician who was self-taught and had an uncanny mathematical manipulative ability. Ramanujan was unable to pass his school examinations in India, and could only obtain a clerk's position in the city of Madras. However, he continued to pursue his own mathematics, and sent letters to three ...
The Man Who Knew Infinity is a biography of Srinivasa Ramanujan by Robert Kanigel. It was published in 1991 and later was turned into a movie starring Dev Patel as Srinivasa Ramanujan and Jeremy ...
Srinivasa Ramanujan (1887-1920), the man who reshaped twentieth-century mathematics with his various contributions in several mathematical domains, including mathematical analysis, infinite series, continued fractions, number theory, and game theory is recognized as one of history's greatest mathematicians. Leaving this world at the youthful age of 32, Ramanujan made significant contributions ...
Srinivasa Ramanujan was an Indian mathematician who made significant contributions to a number of fields, including number theory, analysis, and combinatorics. He was born in 1887 in Erode, Tamil Nadu, and began showing signs of his mathematical genius at a young age. When he was just 12 years old, he taught himself advanced trigonometry from a ...
The Beginning of the Story. Needless to say, there's a human story behind this: the remarkable story of Srinivasa Ramanujan.. He was born in a smallish town in India on December 22, 1887 (which made him not "about 23", but actually 25, when he wrote his letter to Hardy).His family was of the Brahmin (priests, teachers, …) caste but of modest means.
Answer 1: Srinivas Ramanujan is famous for his discoveries that have influenced several areas of mathematics. Furthermore, he is famous for his contributions to number theory and infinite series. Moreover, he came up with fascinating formulas that facilitate in the calculation of the digits of pi in unusual ways.
Srinivasa Ramanujan FRS (1887 - 1920) was a self-taught Indian mathematical genius who made numerous contributions in several mathematical fields including mathematical analysis, infinite series, continued fractions, number theory and game theory.Ramanujan provided solutions to mathematical problems that were then considered unsolvable. Moreover, some of his work was so ahead of his time ...
Ramanujan number is a natural number that can be represented in two different ways by the sum of the cubes of two numbers. Example, {9 3 +10 3 =1 3 +12 3 =1729} Ramanujan numbers are 1729, 4104, 20683, 39312, 40033 etc. Death of Srinivasa Ramanujan. At 32, Ramanujan died at Kumbakonam, India, on April 26, 1920.
Ramanujan Congruences. Ramanujan obtained three congruences when m is a whole number, p (5m+ 4) ≡ 0 (mod 5), p (7m+ 5) ≡ 0 (mod 7), p (11m+ 6) ≡ 0 (mod 11). Hardy and E.M. Wright wrote, he was first to led the conjecture and then to prove, three striking arithmetic properties associated with the moduli 5, 7 and 11.".
Srinivasa Ramanujan was born on 22 December, 1887, to a poor Brahmin family in Erode, a small village in Tamil Nadu, India. He grew up in Kumbakonam town, near Chennai, where his father was employed as a clerk in a cloth merchant's shop. He was an exceptionally good student and won a number of merit certificates and awards.
Rather than do a strict biography, I thought that Bill Gates' evolving image over the decades presented an interesting opportunity to examine some of the broader themes in society, how we are ...
4. He reminds you of your high school history teacher for a reason. Mr. Walz taught high school social studies and geography — first in Alliance, Neb., and then in Mankato, Minn. — before ...